145. Squares

Given the length of n segments. What is the maximum number of squares can be constructed? Each side of a square must be constructed from only one segment.

Input. The first line contains the number of segments n (1 ≤ n ≤ 10⁶). The second line contains n integers – the length of segments with values no more than 100.

Output. Print the maximum number of squares that can be constructed from the given segments.

Sample input	Sample output
9 2 2 4 2 3 2 1 2 4	1

SOLUTION

counting sort

Algorithm analysis

Let we have k segments of the same length. Then you can make k / 4 squares out of them. The lengths of the segments vary from 1 to 100. Count the number of segments of length i (1 ≤ i ≤ 100) in cnt[i]. Then the maximum possible number of squares that can be made out of the given segments is

cnt[1] / 4 + cnt[2] / 4 + …. + cnt[100] / 4

Example

Consider the state of the cnt array after counting sort.

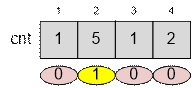
From segments of length 2, you can make 5 / 4 = 1 square. It is impossible to make squares out of the remaining lengths of the line segments.

Algorithm realization

Declare the array for counting.

int cnt[101];

Read the input data. Perform counting sort. In the cell cnt[i], count the number of segments of length i.

scanf("%d",&n);

for(j = 0; j < n; j++)

{

scanf("%d",&i);

cnt[i]++;

}

In the variable res, count the number of squares that can be made.

res = 0;

for(i = 1; i <= 100; i++)

res += cnt[i] / 4;

Print the answer.

printf("%d\n",res);

Java realization

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int cnt[] = new int[101];

for(int i = 0; i < n; i++)

{

int val = con.nextInt();

cnt[val]++;

}

int res = 0;

for(int i = 1; i <= 100; i++)

res += cnt[i] / 4;

System.out.println(res);

con.close();

}

}